Daftar Rumus Matematika SD Kelas 6 Lengkap

                                                       

Untuk memudahkan sobat hitung belajar matematika di rumah, khusunya yang masih menimba ilmu di kelas 6 Sekolah Dasar, berikut kami sajikan rangkuman lengkap rumus-rumus matematika yang sering digunakan dalam soal. Umumnya rumus matematika kelas 6 SD sedikit banyak mencakup juga rumus-rumus dari kelas 4 dan kelas 5. Semoga bisa membantu dalam persiapan menghadapi ujian nasional tahun 2016 nanti.

Materi Rumus Matematika SD Kelas 6

• Operasi Bilangan Bulat
• Operasi Hitung Bilangan Campuran
• KPK dan FPB pada Dua dan Tiga Bilangan
• Menentukan Akar Pangkat 3 Bilangan Kubik
• Volume dan Waktu
• Menghitung Luas Bangun Datar
• Rumus Volume Bangun Ruang Kelas 6 SD
• Pengolahan Data Kelas 6 SD
• Operasi Hitung Pecahan
• Skala
• Sistem Koordinat
• Mengolah dan Menyajikan Data

Operasi Bilangan Bulat

1. Sifat Komutatif atau Pertukaran

Sifat komutatif pada penjumlahan
rumus bentuk umum: a + b = b + a
Contoh:
7 + 8 = 8 + 7 = 15
20 + 15 = 15 + 20 = 35

Sifat komutatif pada perkalian
rumus bentuk umum: a x b = b x a
Contoh:
4 x 5 = 5 x 4 = 20
12 x 3 = 12 x 3 = 36

2. Sifat Asosiatif atau Pengelompokan

Sifat asosiatif pada penjumlahan
bentuk umum : (a+b) + c = a + (b +c)
Contoh:

(12 + 3) + 7	= 12 + (3 +7)
15 + 7	= 12 + 10
22	= 22

Sifat asosiatif pada perkalian
bentuk umum : (a xb) x c = a x (b x c)
Contoh:

(4 x 3) x 5	= 4 x (3 x 5)
12 x 5	= 4 x 15
60	= 60

3. Sifat Distribusif atau Penyebaran

Sifat distributif perkalian terhadap penjumlahan
rumus bentuk umumnya adalah : a × (b + c) = (a × b) + (a × c)
Contoh:

3 x (5 + 7)	= 3 x 5 + 3 x 7
	= 15 + 21
	= 36

Sifat distributif perkalian terhadap pengurangan
Contoh:

3 x (9 – 2)	= 3 x 9 – 3 x 2
	= 27 – 6
	= 21

Operasi Hitung Bilangan Campuran

Ketentuan operasi hitung:

– Jika ada kurung kerjakan yang di dalam kurung terlebih dahulu
– jika tidak ada kurung, perkalian dan pembagian di dahulukan adari pada penjumlahan dan pengurangan

Contoh:
7500 – 30 × 50 : 3 + 250
= 7500 – 500 – 250
= 6750

336 : 12 x 20 – (235 + 146)
= 336 : 12 x 20 – 381
= 28 x 20 – 381
= 560 – 381
= 179

KPK dan FPB pada Dua dan Tiga Bilangan

Menentukan FPB dua bilangan
Cara menentukan FPB dua bilangan
– Cari faktor pad masing-masing bilangan
– Tentukan faktor persekutuan dari kedua bilangan
– Kalikan faktor persekutuan (faktor yang sama) yang memiliki pangkat paling kecil

18 = 2 x 32
27 = 33
—————
faktor yang sama adalah 3, yang berpangkat paling kecil adalah 32 = 9

Menentukan KPK dua Bilangan
Cara menentukan KPK dua bilangan
– Cari faktor prima dari masing-masing bilangan
– kalikan semua faktor, faktor yang sama dipilih pangkat yang laing tinggi
Contoh
KPK 12 dan 15
Faktor Prima
12 = 22 x 3
15 = 3 x 5
KPK = 22 x 3 x 5 = 60
untuk KPK dan FPB 3 bilangan caranya sama.

Baca Juga : Advanced KPK dan FPB

Menentukan Akar Pangkat 3 Bilangan Kubik

13 dibaca satu pangkat tiga = 1 × 1 × 1 = 1
23 dibaca dua pangkat tiga = 2 × 2 × 2 = 8
33 dibaca tiga pangkat tiga = 3 × 3 × 3 = 27
43 dibaca empat pangkat tiga = 4 × 4 × 4 = 64
53 dibaca lima pangkat tiga = 5 × 5 × 5 = 125

1, 8, 27, 64, 125, dan seterusnya adalah bilangan kubik atau bilangan pangkat 3

Penjumlahan dan Pengurangan

23 + 33 = (2 × 2 × 2) + (3 × 3 × 3)
= 8 + 27
= 35

63 – 43 = (6 × 6 × 6) – (4 × 4 × 4)
= 216 – 64
= 152

Perkalian dan Pembagian

23 × 43 = (2 × 2 × 2) × (4 × 4 × 4)
= 8 × 64
= 512

63 : 23 = (6 × 6 × 6) : (2 × 2 × 2)
= 216 : 8
= 27

Volume dan Waktu

Hubungan Satuan Volume

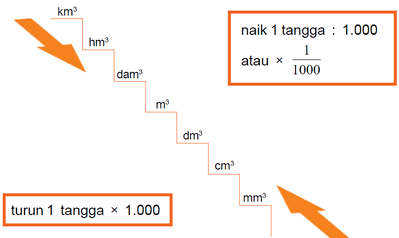
Contoh
1 m3 = 1.000 dm3 = 1.000.000 cm3 = 1.000.000.000 mm3
1.000.000.000 m3 = 1.000.000 dam3 = 1.000 hm3 = 1 km3

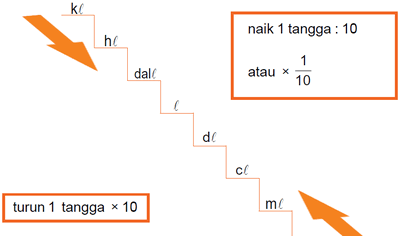
Volume dalam Liter

Satuan Waktu

1 abad	= 100 tahun
1 windu	= 8 tahun
1 tahun	= 12 bulan
1 tahun	= 52 minggu
1 bulan	= 4 minggu
1 bulan	= 4 minggu
1 minggu	= 7 hari
1 dasawarsa	= 10 tahun
1 dekade	= 10 tahun
1 milenium	= 1000 tahun
1 hari	= 24 jam
1 jam	= 60 menity
1 menit	= 60 detik

Menghitung Luas Bangun Datar

Bangun	Rumus Luas
Persegi Panjang	L = Panjang x Lebar
Jajar Genjang	L = Alas x Tinggi
Belah Ketupat	L = ½ x d1 x d2
Layang-Layang	L = ½x d1 x d2
Trapesium	L = ½ t × (a+b)
Segitiga	L = ½ alas x tinggi
Persegi	L = sisi x sisi = s2
Lingkaran	L = phi x r2

Rumus Volume Bangun Ruang Kelas 6 SD

Nama Bangun Ruang	Rumus Volume
Prima tegak segitiga	V = Luas alas x Tinggi
Tabung	V = phi r2 x t

Pengolahan Data Kelas 6 SD

Pengurutan Data

6 8 7 5 9 8 8 6 9 7
10 6 6 8 8 7 7 5 5 10
4 5 9 9 5 4 4 5 6 10

Jika diurutkan dengan tabel dan frekuensi menjadi

Nilai	Banyaknya (Frekuensi)
4	3
5	6
6	5
7	4
8	5
9	4
10	6
Total	30

Menafsirkan Data:

– Nilai Terkceil
– Nilai Terbesar
– Nilai Rata-rata, dan sebagainya

Operasi Hitung Pecahan

Menyederhanakan Pecahan

Menyederhanakan pecahan dapat dilakukan dengan membagi pembilan dan penyebut dengan menggunakan bilangan yang sama contoh:

Mengurutkan Pecahan

Langkah-langka mengurutkan pecahan
– Samakan penyebut pecahan yang akan diurutkan
– Penyamaan bisa sobat lakukan dengan menggunakan KPK
– Jika penyebutnya sudah sama tinggal urutkan pembilangnya dari yang terkecil atau yang terbesar.

Mengubah Bentuk Pecahan ke desimal dan sebaliknya

Jadikanlah penyebutnya kelipatan sepuluh kemudian tarik koma kekiri sesuai dengan angka nol di penyebutnya

Untuk lebih lengkapnya tentang cara cepat mengubah pecahan biasa ke bilangan desimal atau sebaliknya bisa sobat baca di mengubah pecahan.

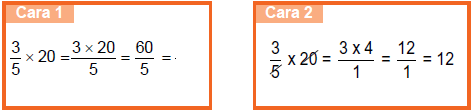
Mengalikan Pecahan dengan Bilangan Bulat

Contoh:

Menjumlahkan dan Mengurangkan Pecahan

Untuk dapat menambahkan dan mengurangkan pecahan terlebih dahulu samakan penyebutnya.

Mengalikan dan Membagi Pecahan

Mengalikan pecahan cukup mudah. Pembilang dikalikan pembilang. Penyebut dikalikan penyebut. Kalau bisa disederhanakan maka sederhanakanlah.

Pembagian pecahan sama dengan mengalikan dengan kebalikan bilangan pecahan pembagi.

Skala

• Rumus Skala = Jarak pada gambar (peta) / jarak sebenarnya
• Rumus Jarak Sebenarnya = Jarak pada gambar (peta) / skala
• Rumu  Jarka pada gambar = Jarak sebenarnya x skala

Sistem Koordinat

• Sebuah bidang koordinat cartesius terbetuk oleh dua buah sumbu. Sumbu tegak (sumbu y) dan sumbu mendatar (sumbu x).
• Dari titik nol sumbu tegak ke atas dan sumbu mendatar ke kanan mempunyai nilai positif.
• Dari titik nol sumbu tegak ke bawah dan sumbu mendatar ke kiri mempunyai nilai negatif.
• Mencari titik koordinat suatu objek didapat dengan mencari letak pada sumbu x ke kanan atau ke kiri dengan letak pada sumbu y ke atas atau ke bawah.
• Sumbu x juga disebut dengan absis (x) dan sumbu y disebut dengan ordinat (y).

Mengolah dan Menyajikan Data

Rata-Rata : Rata-rata dicari dengan menjumlahkan semua sample dibagi dengan jumlah sampel.
Nilai Maksimum : Adalah nilai tertinggi dari semua data yang ada.
Nilai Minimum : Nilai terkecil atau terendah dari semua data.
Modus : Nilai yang paling banyak muncul

Penyajian data dapat dilakukan dengan bentuk:

penyajian data dalam bentuk diagram lingkaran

a. Tabel
b. Diagram Batang
c. Diagram Lingkaran
d. Bentuk Lain

Sumber : http://rumushitung.com/2015/08/07/daftar-rumus-matematika-sd-kelas-6-lengkap/