Blogku Jendela Duniaku: Kumpulan Rumus Matematika SD Kelas 5

Kumpulan Rumus Matematika Kelas 5 SD

Di sekolah dasar anak lebih banyak dikenalkan pada matematika dasar sebagai pondasi untuk belajar matematika yang lebih kompleks di kemudian hari. Jika penulis amati, materi matematika untuk sekolah dasar tidak lepas dari materi teori bilangan, bilangan bulat, pecahan, pengukuran dan juga aritmatika sosial sederhana. Kali ini rumushitung.com akan membagikan rangkuman kumpulan rumus matematika untuk kelas 5 sekolah dasar. Semoga bisa membantu belajar sobat-sobat atau membantuk bapak/ibu guru dalam mengajar murid didiknya. Materi matematika kelas 5 SD membahas mengenai bilangan bulat, pengukuran, bandun datar (terutama luas), volume bangun ruang kubus dan balok, pecahan, dan beberapa materi pokok lain.

Daftar Konten rumus matematika kelas 5 SD

BILANGAN BULAT

a. Sifat-sifat Operasi Bilangan Bulat

Sifat Operasi Komutatif
a. Sifat komutatif pada penjumlahan
a + b sama dengan b + a
15 + 5 = 20
5 + 15 = 20

b. Sifat komutatif pada perkalian
a x b sama dengan b x a
3 x 4 = 12
4 x 3 = 12

Sifat Operasi Asosiatif
a. Asosiatif pada penjumlahan
a + (b + c) sama dengan (a + b) + c
1 + (2 + 3) = 6
(1 + 2) + 3 = 6

b. Asosiatif pada perkalian
a x ( b x c) sama dengan (a x b) x c
2 x (3 x 5) = 30
(2 x 3) x 5 = 30

Sifat Distributif
a. Sifat distributif perkalian terhadap penjumlahan
a x ( b+c) sama dengan a x b + a x c
2 x (3+4) = 2 x 3 + 2 x 4 = 6 + 8 = 14

b. Sifat distributif perkalian terhadap pengurangan
a x (b -c) = a x b – a x c
2 x (5-1) = 2 x 5 – 2 x 1 = 10 – 2 = 8

Untuk sifat operasi bilangan yang lebih lengkap sudah pernah kita bahas di postingan rumus matematika lengkap kelas 6 SD.

b. Pembulatan Bilangan

Membulatkan ke satuan terdekat
– Angka di belakang koma kurang dari 0,5 maka dibulatkan menjadi nol. Contoh 92,4 dibulatkan menjadi 92
– Angka di belakang koma lebih dari 0,5 atau sama dengan 0,5 maka dibulatkan menjadi 1. Contoh 92,7 dibulatkan menjadi 93

Membulatkan ke puluhan terdekat
– Angka satuan kurang dari 5 dibulatkan menjadi 0 contoh 954 dibulatkan menjadi 950
– Angka satuan yang lebih dari atau sama dengan 5 dibulatkan ke atas menjadi 1 puluhan. contoh 958 dibulatkan menjadi 960.

Membulatkan ke ratusan terdekat
– Angka puluhan yang kurang dari 5 dibulatkan menjadi nol contoh 1547 dibulatkan menjadi 1500
– Angka puluhan yang lebih dari atau sama dengan 5 dibulatkan menjadi 1 angka ratusan. Contoh 1898 dibulatkan menjadi 1900.

Membulatkan ke ribuan terdekat
– Angka ratusan yang kuran dari 5 dibulatkan menjadi nol contoh 425.300 dibulatkanmenjadi 525.000
– Angka ratusan yang lebih dari atau sama dengan 5 dibulatkan menjadi 1 ribuatn. Contoh 230.700 dibulatkan menjadi 231.000

KPK dan FPB

untuk materi KPK dan FPB sudah dibahas lengkap pada postingan KPK dan FPB. Intinya adalah belajar bilangan prima dan faktorisasi prima untuk menentukan kelipatan persekutuan terkecil atau faktor pembagi terbesar dari dua atau lebih bilangan bulat.

Operasi Hitung Campuran pada bilangan bulat
– Penjumlahan dan pengurangan adalah operasi setara maka pengerjaannya mulai dari kiri.
– Pembagian dan perkalian adalah operasi setara maka pengerjaannyapun dimulai dari kir
– Perkalian dan pembagian lebih tinggi tingkatnnya daripada penjumlahan dan pengurangan sehingga didahulukan dalam pengerjaan.

Contoh

– Perkalian dan pembagian dua bilangan yang memiliki tanda yang sama akan mengahsilkan bilangan positif
– Perkalian dan pembagian dua bilangan yang berbeda tanda akan menghasilkan bilangan negatif

PENGUKURAN

a. Mengukur Waktu

Ada dua pengukuran waktu yakni menggunakan notasi 12 jam dan dengan menggunakan notasi 24 jam.

Notasi 12 Jam	Notasi 24 Jam

Pukul 07.00 malam	Pukul 19.00 (12 + 7)

b. Operasi hitung dengan waktu

1 jam = 60 menit
1 menit = 60 detik
1 jam = 60 x 60 = 3.600 detik

c. Mengukur Sudut

– sudut lancip < 90º
– sudut tumpul > 180º
– sudut sikut-siku = 180º
– pengukuran sudut bisa dilakukan dengan alat yang disebut dengan busur

d. Menentukan jarak dan kecepatan

kecepatan = jarak : waktu
waktu = jarak : kecepatan
jarak = kecepatan x jarak

1 mil = 1,86 km
1 inchi = 2,54 cm
1 feet = 12 inchi = 30,48 cm
1 mil = 5280 feet

LUAS BANGUN DATAR

untuk di kelas 5 SD, bangun datar yang dibahas adalah trapesium dan layang-layang.
Trapesium adalah sebuah segiempat yang memiliki sepasang sisi yang berhadapan sama panjang (hanya dua sisi, kalau persegi atau persegi panjang 2 pasang sisi)
Layang-layang adalah bangun segiempat yang terbentuk dari dua buah segitiga sama kaki yang alasnya saling berimpit dan membelakangi.

Nama Bangun Datar	Rumus Luas
Trapesium	= ½ x jumlah sisi sejajar x tinggi
Layang-layang	= ½ x Diagonal 1 x Diagonal 2

VOLUME BALOK DAN KUBUS

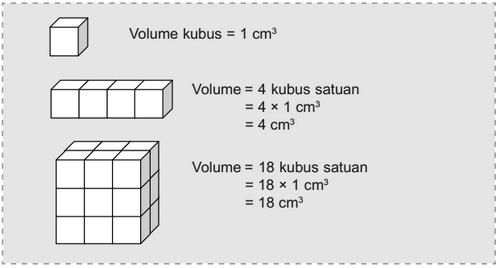
a. Menentukan volume kubus dan balok dengan kubus satuan

Salah satu alternatif mencari volume sebuah kubus atau balok adalah dengan menggunakan kubus satuan. Perhatikan contoh berikut:

menghitung volume kubus dan balok menggunakan balok satuan

b. Menentukan volume kubus dan balok dengan rumus

Nama Bangun	Rumus Volume
Kubus	= s x s x s
Balok	= p x l x t

s = sisi kubus
p = panjang balok
l = lebar balok
t = tinggi balok

c. Satuan Volume
1 km3 = 1.000.000 dam3 = 1.000.000.000 m3
1 m3 = 1.000 dm3 = 1.000.000 cm3
1 liter = 1 dm3
1 mililiter = 1 cm3 = 1 cc

berikut grafiik tangga satuan volume dalam kubik dan liter

PECAHAN

1. Menjadikan pecahan biasa ke bentuk persen

untuk mengubah pecahan ke bentuk persen dilakukan dengan mengubah penyebutnya ke bentuk 100.
Contoh
3/4 –> 75/100 –> 75%
1/2 –> 50/100 –> 50%
1/4 –> 25/100 –> 25%

2. Mengubah pecahan desimal menjadi pecahan biasa

untuk materi ini selengkapnya bisa sobat baca di postingan mengubah pecahan desimal ke pecahan biasa.

3. Operasi hitung pecahan

– menjumlahkan dan mengurangkan pecahan dengan penyebut sama
jika pecahan penyebutnya sudah sama tinggal ditambahkan saja. contoh:
1/5 + 2/5 = 3/5
1/7 + 5/7 = 6/7

– menjumlahkan dan mengurangkan pecahan dengan penyebut berbeda
penjumlahan pecahan dengan penyebut berbeda harus disamakan penyebutnya dengan menggunakan KPK kedua penyebutnya. contoh:
1/5 + 1/3 = 3/15 + 5/15 = 8/15
*KPK 5 dan 3 adalah 15

1/6 + 1/5 = 5/30 + 6/30 = 11/30
*KPK 6 dan 5 adalah 30

– menjumlahkan dan mengurangkan pecahan desimal

– perkalian pecahan (baca DI SINI)
– pembagian pecahan (baca DI SINI)

PERBANDINGAN DAN SKALA

– Perbandingan sama prinsipnya dengan pembagian. 5 dibanding 3 sama seperti 5/3
– Perbandingan suhu Celcius : Reamur : Fahrenheti = 5 : 4 : 9 (+32)
– Skala adalah perbandingan jarak pada peta dengan jarak sebenarnya

SIFAT-SIFAT BANGUN DATAR DAN BANGUN RUANG

Beberapa bangun ruang yang diperkenalkan dalam rumus matematik kelas 5 SD diantaranya:

Sifat-sifat persegi

– memiliki 4 sisi sama panjang
– memiliki 4 sudut sama besar
– mempunyai 4 sudut dan siku-siku
– sisi yang berhadapan sejajar dan sama panjang

Sifat-sifat persegi panjang

– memiliki 2 pasang sisi. Masing-masing pasang sama panjang
– memiliki 4 sudut siku-siku
– mempunyai dua buah diagonal bidang yang sama panjang

Sifat-sifat segitiga sama kaki

– memiliki dua sisi (kaki) yang sama panjang
– memiliki dua buah sudut yang sama besar

Sifat-sifat segitiga sama sisi

– ketiga sisinya sama panjang
– memiliki 3 buah sudut sama besar 60º

Sifat-sifat segitiga siku-siku

– memiliki satu buah sudut siku-siku 45º
– berlaku hukum phytagoras

Sifat-sifat segitiga lancip

– memiliki sudut-sudut yang besarnya kurang dari 90º

Sifat-sifat segitiga tumpul

– memiliki sudut lebih dari 90º tetapi masih kurang dari 180º

Sifat-sifat jajar genjang

– sisi-sisi yang berhadapan sejajar dan sama panjang
– sudut-sudut yang berhadapan sama besar
– kedua diagonalnya berpotongan saling membagi dua sama panjang
– jumlah sudut-sudut yang berdekatan sama dengan 180º

Sifat-sifat trapesium sama kaki

– memiliki 2 sisi yang sama panjang
– memiliki sepasang sisi sejajar (beda panjang)
– memiliki 2 pasang sudut. Masing-masing pasan besarnya sama.

Sifat-sifat trapesium siku-siku

– memiliki sudut siku-siku sebanyak 2 buah
– memiliki sepasang sisi yang sejajar (beda panjang)

Sifat-sifat layang-layang

– memiliki satu sumbu simetri
– memiliki 2 pasang sisi sama panjang
– memiliki dua pasang sudut yang berhadapan dan masing-masing pasang sama besar

Sifat-sifat belah ketupat

– semua sisi sama panjang
– kedua diagonal belah ketupat merupakan sumbu simetri
– sudut-sudut yang berhadapan sama besar
– diagonal-diagonal belah ketupat saling tegak lurus dan berpotongan

Sifat-sifat lingkaran

– memiliki satu titik pusat
– memiliki garis tengah yang panjangnya 2 kali jari-jari
– memiliki sumbu simetri yang jumlahnya tidak terhingga

Sifat-sifat prisma tegak segiempat

– memiliki 6 sisi berbentuk persegi atau persegi panjang
– memiliki sisi yang berhadapan sama luasnya
– memiliki 12 rusuk dimana rusuk yang sejajar sama panjang
– memiliki 8 titik sudut.

Sifat-sifat prisma tegak segitiga

– memiliki 9 buah rusuk
– memiliki 6 buah titik sudut
– memilik 5 buah sisi
– alas dan atapnya berbentuk segitiga

Sifat-sifat limas segiempat

– memiliki 8 buah rusuk
– memiliki 5buah sisi dan 5 buah titik sudut
– memiliki titik puncak yang merupakan pertemuan 4 buah segitiga.
– alasnya berbentuk segiempat.

Sifat-sifat limas segitiga

– memiliki 6 buah rusuk
– memiliki 4 buah sisi
– memiliki 4 buat titik sudut
– alasnya berupa segitiga

Sifat-sifat kerucut

– alasnya berupa lingkaran
– memiliki sisi lengkung
– memiliki titik puncak

Simetri lipat dan simetri putar

untuk materi simetri lipat dan simetri putar kelas 5 SD bisa anda baca di SINI.

Sekian dulu sobat rangkuman rumus matematika kelas 5 SD dari rumushitung.com. Semoga bisa membantu sobat belajar di rumah. Selamat belajar.

Sumber : http://rumushitung.com/2015/11/11/rumus-matematika-sd-kelas-5/

Blogku Jendela Duniaku

Kumpulan Rumus Matematika SD Kelas 5